MVEE(Minimun Volumn Enclosing Ellipsoids)
根据MVEE问题的最优性条件,只需要求解对偶问题就可以得到原问题的最优解,对偶问题如下:
$$
\begin{align}
&\text{max}_ {u \in \mathcal{R}^m} \quad & g(u)& \triangleq \text{lndet}(XUX^T) \tag{1} \\
&\text{s.t.} \quad &\mathbf{1}^Tu&=1 \nonumber \\
&&u&\ge0
\end{align}
$$
对于问题$(1)$可以用FW算法和WA算法求解。
FW算法
FW算法(Frank 1956)是一种特殊的一阶优化算法,在某些情况下也可以说是坐标下降算法,这个算法的主要思想是用一阶泰勒展示近似目标函数$f(x)$,来选择每一步迭代的下降方向。
考虑如下这个问题,其中$\mathcal{X}$是紧凸集,$f(x)$是凸的可微实值函数。FW算法可以求解这个优化问题:
$$
\begin{align}\text{min} \quad & f(x)\tag{2} \\
\text{s.t.} \quad &x\in \mathcal{X}\nonumber \end{align}
$$
算法
FW algorithm
给定初值$x_k$
步骤1. 下降方向选择问题(通过求解这个子优化问题得到下降方向$s_k$)
$$
\begin{align}\text{min} \quad & s^{T}\nabla f(x_k)\tag{3} \\
\text{s.t.} \quad &s\in \mathcal{X}\nonumber \end{align}
$$步骤2. 步长选择(通过求解这个子问题得到最优下降步长,或者使用事先设定的步长)
$$
\begin{align}\text{min} \quad & f(x_k+\gamma(s_k-x_k)) \tag{4}\\
\text{s.t.} \quad & 0\le\gamma\le1 & \nonumber\end{align}
$$步骤3. 更新
$$
\begin{align} x_{k+1}=x_k+\gamma(s_k-x_k)\tag{5} \end{align}
$$步骤4. 判断是否满足停止条件,若不满足回到步骤1
算法的解释
$f(x)$在$x_k$的一阶泰勒展式为$$\begin{align}f(x)=f(x_k)+(x-x_k)^T\nabla f(x_k)+O(x-x_k)\tag{6}\end{align}$$用$(6)$等号右边前两项近似$f(x)$,因为$x_k$是给定常数,可以得到优化问题$(3)$,FW算法的思想即为用近似问题的最优解的方向$s_k-x_k$作为原问题的下降方向。
将$(4)$改写为
$$
x_{k+1}=(1-\gamma)x_k+\gamma s_k \tag{7}
$$
因为$0\le\gamma\le1$所以$x_{k+1}$是$x_k$与$s_k$的凸组合。这样更新步在一些特定问题中与梯度下降算法与坐标下降算法相比具有优势。
求MVEE的近似解的FW算法(Todd 2016)
因为$(1)$的约束是单位单纯形,所以FW算法中$(3)$的解一定在单纯形的顶点上,也就是$ s_k=e_i $,$i$为$ g(u) $在$u_k$的梯度中最小的一个元素的下标。更新得到的$u_k$一定还在单位单纯形上。而梯度下降算法与坐标下降算法是不能保证每一步更新得到的$u_k$仍在单纯形上。
FW algorithm
给定初值$u$满足$(7)$的约束与$\epsilon\gt0$,计算$g(u)$的梯度和$XUX^T$的Cholesky分解
$$
w\triangleq\nabla g(u)
$$
步骤1. 计算
$$
\epsilon_+=\max_h\frac{(w_h-n)}{n}
$$
记$h=i$取得最大值,如果$\epsilon_+ \lt\epsilon$,停止:得到近似解u步骤2. 计算
$$
\lambda \triangleq\frac{w_i-n}{(n-1)w_i}
$$
更新 $ u \leftarrow (1+\lambda )^{-1} (u+\lambda e_i)$步骤3. 更新$w$与$XUX^T$的Cholesky分解,回到步骤1
WA算法
回到下降方向的选择问题,在FW算法中下降方向指向线性近似问题的最优解。从另一个角度来考虑,下降方向也可以指向线性近似问题的最差解的负方向(如果这个解存在的话),也就是远离最差的解。WA算法(Atwood)综合考虑了这两种思想来选择下降方向。
WA algorithm
给定初值$u$满足$(7)$的约束与$\epsilon\gt0$,计算$g(u)$的梯度和$XUX^T$的Cholesky分解
$$
w\triangleq\nabla g(u)
$$
步骤1. 计算
$$
\epsilon_+=\max_h\frac{(w_h-n)}{n}, \,\epsilon_-=\max_h \left\{ \frac{(n-w_h)}{n} : u_h \gt 0 \right\}
$$
记$h=i$使得$\epsilon_+$取得最大值,$h=j$使得$\epsilon_-$取得最大值。如果$\max \{\epsilon_+,\epsilon_- \} \lt\epsilon$,停止:得到近似解u;否则,如果$\epsilon_+\gt \epsilon_-$,前往步骤2;如果$\epsilon_+\lt \epsilon_-$,前往步骤3。步骤2. 计算
$$
\lambda \triangleq\frac{w_i-n}{(n-1)w_i}
$$
更新 $ u \leftarrow (1+\lambda )^{-1} (u+\lambda e_i)$,前往步骤4。步骤3.计算
$$
\lambda \triangleq\frac{w_j-n}{(n-1)w_j}
$$
令$\lambda=\max\{-u_j,\lambda\}$,更新 $ u \leftarrow (1+\lambda )^{-1} (u+\lambda e_j)$,前往步骤4。步骤4. 更新$w$与$XUX^T$的Cholesky分解,回到步骤1
一个简单的例子
$$
X=
\begin{bmatrix}
&-1&-1&1&2& \\
&1&-1&-1&2&
\end{bmatrix}
$$
如果考虑KY初始化方法,得到出初值$u=(1/2;0;0;1/2) \text{or} (0;0;1/2;1/2)$ 这两个都是最优解,FW算法与WA算法都立刻终止了。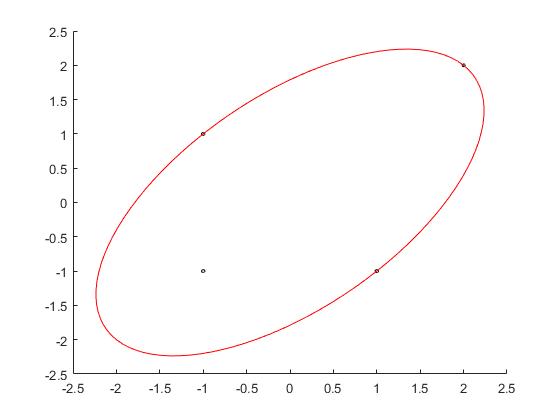
如果考虑K初始化方法$u=(1/4;1/4;1/4;1/4)$。
FW算法效果如下图,收敛速度慢,100次迭代后仍未停止:
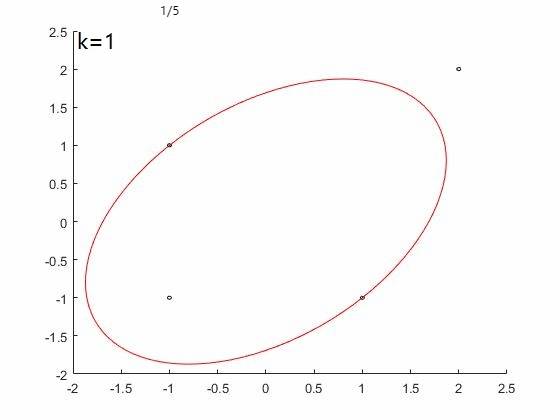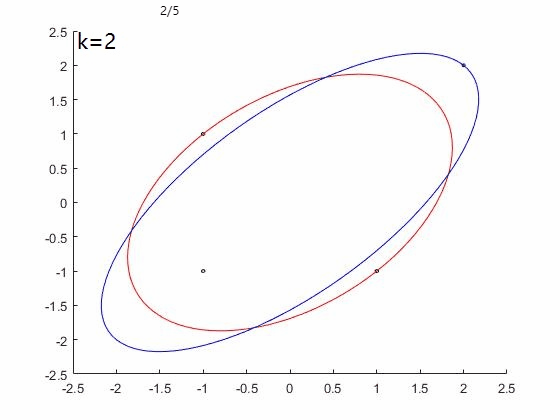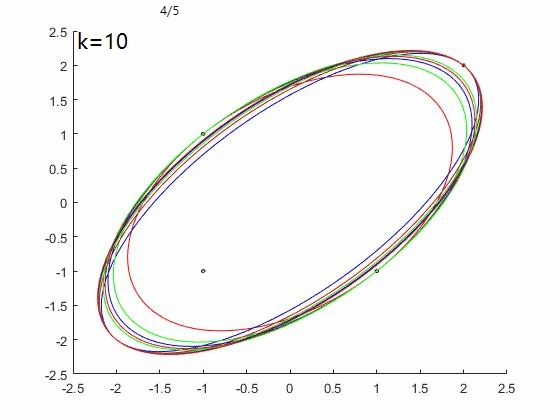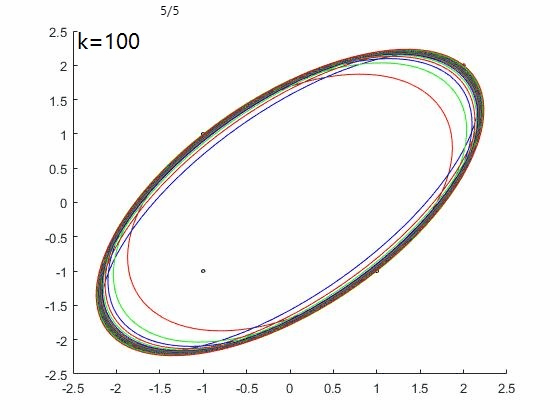
WA算法效果如下图,三次迭代后终止,并得到最优解:
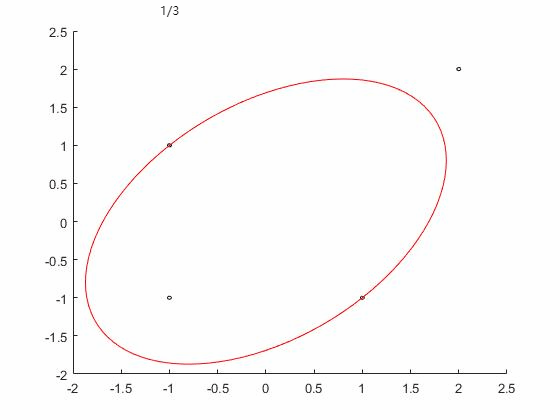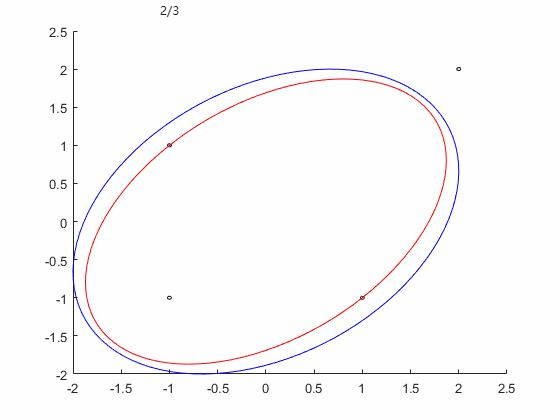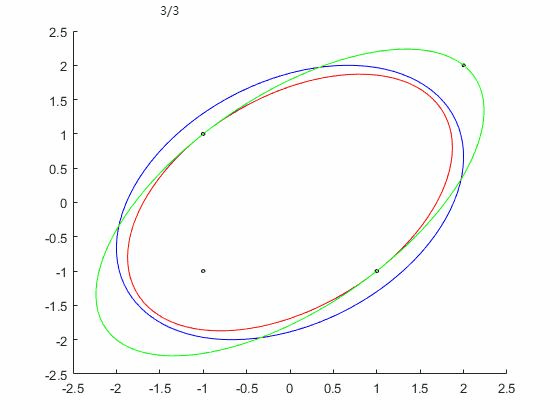
代码来源为Michael J. Todd
[1] Frank, Marguerite, and Philip Wolfe. “An algorithm for quadratic programming.” Naval Research Logistics (NRL) 3.1‐2 (1956): 95-110.
[2] Todd, M.J. Minimum volume ellipsoids: theory and algorithms. New York: Society for Industrial and Applied Mathematics, 2016. 26-29.